Data Matching

Data matching is the process of identifying which records from data sources correspond to the same real-world entity.

Why is it hard?

Each data matching domain has special challenges when trying to match records from different sources to the real-world entity or object.

For example:

Record matching approaches

There are two main approaches to record matching:

• Equality-based: Two records are matched if some or all the fields are equal (or almost equal)
• Pairwise comparison: Calculate the similarity score between record pairs; two records are matched if their similarity score is above a specified threshold.

Equality-based matching is adequate for straight-forward record matching. However, for equality-based matching, it becomes increasingly difficult to express complex record matching logic as a boolean matched or not matched expression.

Pairwise comparison matching allows more complex record matching logic to be expressed as a numeric score, usually in the range from 0 to 1. A score can be built up by adding independent matching factors and applying normalisation functions to obtain a numeric value that captures the similarity between two records.

Record matching activities are inherently quadratic. Notionally, all records from one data set need to be compared with all records from the other data set, so the total number of comparison is the product of the sizes of the two data sets. For large data sets, the notional number of comparisons can be extremely large.

In practice, all record matching techniques involve an indexing stage designed to reduce the number of comparisons. For equality-based matching, the matching logic can be stated in terms of JOIN and WHERE clauses, which allows the database query analyser to apply database indexing to linearize the comparison complexity. For pairwise comparison, a database query analyser cannot apply indexing to linearize the the comparison complexity. Instead, pairwise comparison uses other indexing techniques to reduce the number of comparisons.

Factil's record matching technology is based on pairwise comparison, which allows us to express complex record matching logic and to detect hard to find matches that would be missed by traditional record matching techniques.

Pairwise comparison approaches

There are three main approaches to pairwise comparison:

• Deterministic algorithms rely on defined patterns and rules for assigning weights and scores for determining similarity.
• Probabilistic matching algorithms rely on statistical techniques for assessing the probability that any pair of records represent the same entity.
• Machine learning algorithms use a wide feature vector to calculate the similarity score, where an optimisation algorithm has been used to determine the ideal weights for this calculation according to a reference training set.

In data matching situations where data quality is reasonably high, deterministic algorithms will often be sufficient. However, in data matching situations where data quality is low, both probabilistic matching and machine learning algorithms provide more techniques for handling missing, inconsistent or incorrect data, as well as statistically sound techniques to evaluate and iteratively improve matching accuracy.

For probabilistic matching and machine learning algorithms, two records are compared on a field-by-field basis to produce a score for each field. The field comparison scores are then combined to get a record comparison score. The technique can be easily extended to use additional fields that are derived from the record pairs or their related data, and to use compound fields that are compared on a subfield-by-subfield basis.

There is a wide range of machine learning approaches that could be applied to record matching. Logistic regression is one of the simpler machine learning approaches. We have found that this approach is quite suitable for a wide range of the record matching situations.

In order to cover a wide range of use cases, Factil has developed both probabilistic matching and logistic regression algorithms for advanced matching of person, relationship and location information.

Probabilistic Matching

With probabilistic matching, the comparison score of a pair of records is based on the estimated probability that a pair of records represent the same entity.

In probability theory, two events are independent if the fact that A occurs does not affect the probability of B occurring. The probability of two independent events A and B is equal to the probability of A multiplied by the probability of B. In probabilistic matching we assume, when matching two records, that the matching of corresponding fields of two records is independent. This means that the probability of a pair of records matching is equal to the product of probabilities of the individual fields matching. To simplify calculations, rather than dealing directly with probability, we use the logarithm of probability.

The log probability of a pair of records matching is equal to the sum of log probabilities of the individual fields matching.

To calculate the probability two fields matching we introduce two key concepts:

• M-probability: probability that the two fields agree given that the pair of records is a true match

For each field, the same M-probability applies for all records. In general terms, the data quality of a field is quantified by its M-probability. For example, an M-probability of 0.95 for Last Name means that the probability that two records belonging to the same person will agree on last name is 0.95

• U-probability: probability that the two fields agree given that the pair of records is NOT a true match

U-probability is often simplified as the chance a field will match for randomly selected records. For each field, the U-probability is specific to value of the field. U-probability is calculated according to the proportion of records with a specific value. For example, a U-probability a common English last name like ‘Smith’ may have a U-probabality of 0.047, but uncommon English surnames like ‘Cornejo’ may have a U-probability of 0.0000034.

For each field, the field score equals:

\[ log \left( \frac{M}{U} \right) \qquad \text{if the field values agree} \]

\[ log \left( \frac{1 - M}{1 - U} \right) \qquad \text{if the field values do not agree} \]

The record score is the sum of the field scores.

Logistic Regression

With logistic regression, the comparison score of a pair of records is based the similarity of a pair of records.

Logistic regression differs from probabilistic matching because it requires a set of pairs of records to be labelled by a human expert as to whether they are a 'match' or 'distinct'. This set of labelled record pairs is known as the Training set. As will be explained below, it is used to pre-calculate a set of field weights and a bias used in the calculation of the record scores.

As with probabilistic matching, for logistic regression, the basic technique for comparing two records is to compare the records on a field-by-field basis, and then combine the field comparison scores to get a record comparison score.

With logistic regression, the field comparison score is a numeric value for either the similarity or distance between the field values being compared. In the calculation of the record score, the field scores are multiplied by their field weights and offset by the bias. If the field comparison score is based on similarity (i.e. more similar field values are given higher scores), then the field weight will be positive. However, if the field comparison score is based on distance (i.e. more dis-similar field values are given higher scores), then the field weight will be negative.

More formally, the record comparison score of a pair of records is calculated by:

1. Multiplying each field score with its field weight and adding these values together to get a sub-total.
2. Adding the bias to get a total score that is centred on zero.
3. Applying a sigmoid function to the total score to get a record comparison score between 0 and 1.

The strength of logistic regression method is that a mathematical optimisation algorithm is used to calculate the ideal set of weights and bias for the labelled training set such that matched pairs are given a score close to 1, and distinct pairs are given a score close to zero.

Logistic Regression has been extensively studied in statistics and machine learning. The Wikipedia article at Logistic Regression gives a good introduction to the area, and links to more in-depth descriptions.

The sigmoid function mentioned above is a standard mathematical function to convert a numerical range centred on zero to a range from 0 to 1. The mathematical formula for the sigmoid function is:

\[S(x) = \frac{1}{1 + e^{-x}}\]

The graph of the sigmoid function is shown below

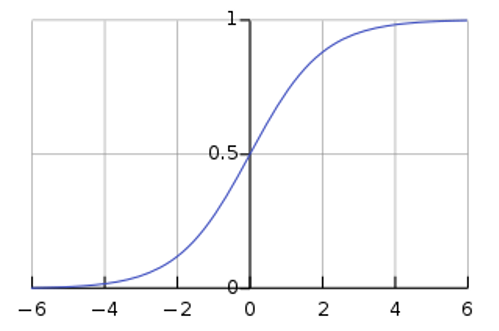
The Wikipedia article at Sigmoid function provides more detail about this function.

Matching Evaluation

To learn more about the evaluation of data matching accuracy, click here.